|
FreeBSD ZFS
The Zettabyte File System
|
|
FreeBSD ZFS
The Zettabyte File System
|
The raidz vdev supports single, double, and triple parity. For single parity, we use a simple XOR of all the data columns. For double or triple parity, we use a special case of Reed-Solomon coding. This extends the technique described in "The mathematics of RAID-6" by H. Peter Anvin by drawing on the system described in "A Tutorial on Reed-Solomon Coding for Fault-Tolerance in RAID-like Systems" by James S. Plank on which the former is also based. The latter is designed to provide higher performance for writes.
Note that the Plank paper claimed to support arbitrary N+M, but was then amended six years later identifying a critical flaw that invalidates its claims. Nevertheless, the technique can be adapted to work for up to triple parity. For additional parity, the amendment "Note: Correction to the 1997 Tutorial on Reed-Solomon Coding" by James S. Plank and Ying Ding is viable, but the additional complexity means that write performance will suffer.
All of the methods above operate on a Galois field, defined over the integers mod 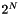 . In our case we choose N=8 for
. In our case we choose N=8 for 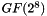 so that all elements can be expressed with a single byte. Briefly, the operations on the field are defined as follows:
so that all elements can be expressed with a single byte. Briefly, the operations on the field are defined as follows:
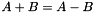
![\[ \begin{array}{rrl} (A \cdot 2)_7 & = & A_6 \\ (A \cdot 2)_6 & = & A_5 \\ (A \cdot 2)_5 & = & A_4 \\ (A \cdot 2)_4 & = & A_3 + A_7 \\ (A \cdot 2)_3 & = & A_2 + A_7 \\ (A \cdot 2)_2 & = & A_1 + A_7 \\ (A \cdot 2)_1 & = & A_0 \\ (A \cdot 2)_0 & = & A_7 \\ \end{array} \]](../../form_3.png)
In C, multiplying by 2 is therefore (a << 1) ^ ((a & 0x80) ? 0x1d : 0). As an aside, this multiplication is derived from the error correcting primitive polynomial 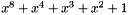 .
.
Observe that any number in the field (except for 0) can be expressed as a power of 2 -- a generator for the field. We store a table of the powers of 2 and logs base 2 for quick look ups, and exploit the fact that 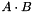 can be rewritten as
can be rewritten as 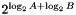 (where '+' is normal addition rather than field addition). The inverse of a field element
(where '+' is normal addition rather than field addition). The inverse of a field element 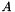 (
( 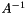 ) is therefore
) is therefore 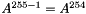 .
.
The up-to-three parity columns, 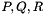 over several data columns,
over several data columns, 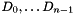 , can be expressed by field operations:
, can be expressed by field operations:
![\[ \begin{array}{rrl} P & = & D_0 + D_1 + \ldots + D_{n-2} + D_{n-1} \\ Q & = & 2^{n-1} D_0 + 2^{n-2} D_1 + \ldots + 2^1 D_{n-2} + 2^0 D_{n-1} \\ & = & ((\ldots((D_0) \cdot 2 + D_1) \cdot 2 + \ldots) \cdot 2 + D_{n-2}) \cdot 2 + D_{n-1} \\ R & = & 4^{n-1} D_0 + 4^{n-2} D_1 + \ldots + 4^1 D_{n-2} + 4^0 D_{n-1} \\ & = & ((\ldots((D_0) \cdot 4 + D_1) \cdot 4 + \ldots) \cdot 4 + D_{n-2}) \cdot 4 + D_{n-1} \end{array} \]](../../form_12.png)
We chose 1, 2, and 4 as our generators because 1 corresponds to the trival XOR operation, and 2 and 4 can be computed quickly and generate linearly- independent coefficients. (There are no additional coefficients that have this property which is why the uncorrected Plank method breaks down.)
See the reconstruction code below for how P, Q and R can used individually or in concert to recover missing data columns.
In the general case of reconstruction, we must solve the system of linear equations defined by the coeffecients used to generate parity as well as the contents of the data and parity disks. This can be expressed with vectors for the original data ( 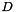 ) and the actual data (
) and the actual data ( 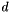 ) and parity (
) and parity ( 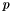 ) and a matrix composed of the identity matrix (
) and a matrix composed of the identity matrix ( 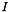 ) and a dispersal matrix (
) and a dispersal matrix ( 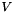 ):
):
![\[ \left[ \begin{array}{c} V \\ I \end{array} \right] \times \left[ \begin{array}{c} D_0 \\ \vdots \\ D_{n-1} \end{array} \right] = \left[ \begin{array}{c} p_0 \\ p_{m-1} \\ d_0 \\ \vdots \\ d_{n-1} \end{array}\right] \]](../../form_18.png)
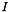 is simply a square identity matrix of size
is simply a square identity matrix of size 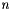 , and
, and 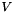 is a vandermonde matrix defined by the coeffecients we chose for the various parity columns (1, 2, 4). Note that these values were chosen both for simplicity, speedy computation as well as linear separability.
is a vandermonde matrix defined by the coeffecients we chose for the various parity columns (1, 2, 4). Note that these values were chosen both for simplicity, speedy computation as well as linear separability.
![\[ \left[ \begin{array}{ccccc} 1 & \ldots & 1 & 1 & 1 \\ 2^{n-1} & \ldots & 4 & 2 & 1 \\ 4^{n-1} & \ldots & 16 & 4 & 1 \\ 1 & \ldots & 0 & 0 & 0 \\ 0 & \ldots & 0 & 0 & 0 \\ \vdots & & \vdots & \vdots & \vdots \\ 0 & \ldots & 1 & 0 & 0 \\ 0 & \ldots & 0 & 1 & 0 \\ 0 & \ldots & 0 & 0 & 1 \end{array} \right] \times \left[ \begin{array}{c} D_0 \\ D_1 \\ D_2 \\ \vdots \\ D_{n-1} \end{array} \right] = \left[ \begin{array}{c} p_0 \\ \vdots \\ p_{m-1} \\ d_0 \\ d_1 \\ d_2 \\ \vdots \\ d_{n-1} \end{array} \right] \]](../../form_20.png)
Note that 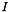 ,
, 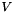 ,
, 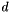 , and
, and 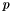 are known. To compute
are known. To compute 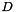 , we must invert the matrix and use the known data and parity values to reconstruct the unknown data values. We begin by removing the rows in
, we must invert the matrix and use the known data and parity values to reconstruct the unknown data values. We begin by removing the rows in 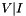 and
and 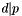 that correspond to failed or missing columns; we then make
that correspond to failed or missing columns; we then make 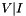 square (
square ( 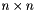 ) and
) and 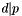 sized
sized 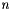 by removing rows corresponding to unused parity from the bottom up to generate
by removing rows corresponding to unused parity from the bottom up to generate 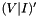 and
and 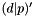 . We can then generate the inverse of
. We can then generate the inverse of 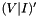 using Gauss-Jordan elimination. In the example below we use
using Gauss-Jordan elimination. In the example below we use 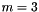 parity columns,
parity columns, 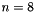 data columns, with errors in
data columns, with errors in 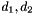 , and
, and 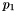 :
:
![\[ (V|I) = \left[ \begin{array}{cccccccc} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 128 & 64 & 32 & 16 & 8 & 4 & 2 & 1 \\ 19 & 205 & 116 & 29 & 64 & 16 & 4 & 1 \\ 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{array}\right] \begin{array}{l} \\ \leftarrow missing \\ \\ \\ \leftarrow missing \\ \leftarrow missing \\ \\ \\ \\ \\ \\ \end{array} \]](../../form_30.png)
![\[ (V|I)' = \left[ \begin{array}{cccccccc} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 19 & 205 & 116 & 29 & 64 & 16 & 4 & 1 \\ 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{array}\right] \]](../../form_31.png)
Here we employ Gauss-Jordan elimination to find the inverse of 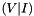 '. We have carefully chosen the seed values 1, 2, and 4 to ensure that this matrix is not singular.
'. We have carefully chosen the seed values 1, 2, and 4 to ensure that this matrix is not singular.
![\[ \left[ \begin{array}{ccccccccccccccccc} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 19 & 205 & 116 & 29 & 64 & 16 & 4 & 1 & & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{array}\right] \]](../../form_33.png)
![\[ \left[ \begin{array}{ccccccccccccccccc} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 19 & 205 & 116 & 29 & 64 & 16 & 4 & 1 & & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{array}\right] \]](../../form_34.png)
![\[ \left[ \begin{array}{ccccccccccccccccc} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & & 1 & 0 & 1 & 1 & 1 & 1 & 1 & 1 \\ 0 & 205 & 116 & 0 & 0 & 0 & 0 & 0 & & 0 & 1 & 19 & 29 & 64 & 16 & 4 & 1 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{array}\right] \]](../../form_35.png)
![\[ \left[ \begin{array}{ccccccccccccccccc} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & & 1 & 0 & 1 & 1 & 1 & 1 & 1 & 1 \\ 0 & 0 & 185 & 0 & 0 & 0 & 0 & 0 & & 205 & 1 & 222 & 208 & 141 & 221 & 201 & 204 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{array}\right] \]](../../form_36.png)
![\[ \left[ \begin{array}{ccccccccccccccccc} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & & 1 & 0 & 1 & 1 & 1 & 1 & 1 & 1 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & & 166 & 100 & 4 & 40 & 158 & 168 & 216 & 209 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{array}\right] \]](../../form_37.png)
![\[ \left[ \begin{array}{ccccccccccccccccc} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & & 167 & 100 & 5 & 41 & 159 & 169 & 217 & 208 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & & 166 & 100 & 4 & 40 & 158 & 168 & 216 & 209 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{array}\right] \]](../../form_38.png)
![\[ (V|I)'^{-1} = \left[ \begin{array}{cccccccc}\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 167 & 100 & 5 & 41 & 159 & 169 & 217 & 208 \\ 166 & 100 & 4 & 40 & 158 & 168 & 216 & 209 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{array}\right] \]](../../form_39.png)
We can then simply compute 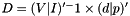 to discover the values of the missing data.
to discover the values of the missing data.
As is apparent from the example above, the only non-trivial rows in the inverse matrix correspond to the data disks that we're trying to reconstruct. Indeed, those are the only rows we need as the others would only be useful for reconstructing data known or assumed to be valid. For that reason, we only build the coefficients in the rows that correspond to targeted columns.
 1.7.3
1.7.3